7-2. 합성곱 계층(convolutional layer)

1. 합성곱 계층 탄생 배경

- 완전 연결 계층 : 데이터의 형상이 무시됨 (ex. 3차원 데이터 -> 1차원으로 줄세워버림)

- 합성곱 계층 : 형상을 유지 (ex, 3차원 데이터를 그대로 사용)

 

2. 합성곱 연산

합성곱 연산의 예. 합성곱 연산을 * 기호로 표기함.

입력 : 4x4

필터(커널) : 3x3

출력 : 2x2

 

합성곱 연산 계산 순서

 

- 합성곱 연산 : 윈도우를 일정 간격으로 이동하며 계산. 윈도우는 위 그림에서 회색 부분에 해당.

- 합성곱 연산 방법 : 왼쪽의 회색 영역(3x3)과 필터(3x3)를 왼쪽 위 원소부터 오른쪽으로 스캔해가며 각 원소를 곱하고 이를 모두 더함. => 단일 곱셈 누산(FMA)

 

 

합성곱 연산의 편향

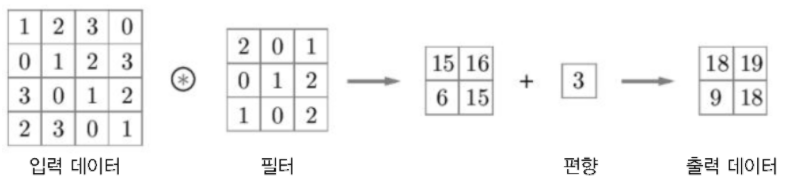
- 편향 : 필터 적용 후의 각 원소에 더해짐. 항상 하나만 존재(1x1).

=> 최종 출력 데이터 생성

 

3. 패딩

 

패딩 1일때의 입력데이터 및 합성곱 연산 결과

- 입력데이터(4x4) + 패딩(1) = 입력데이터(6x6)

- 필터(3x3)

- 출력데이터(4x4) (스트라이드 1 가정 시)

 

- 패딩 사용 이유 : 출력 크기를 조정하기 위함

 

4. 스트라이드

-스트라이드 : 필터를 적용하는 위치의 간격.

스트라이드 2일때의 합성곱 연산 결과 예시

- 위 그림에서, 스트라이드를 2로 적용하면 윈도우(회색 영역)이 두 칸 씩 이동하게 됨.

 

 

5. 3차원 데이터의 합성곱 연산

 

3차원 데이터의 합성곱 연산 순서

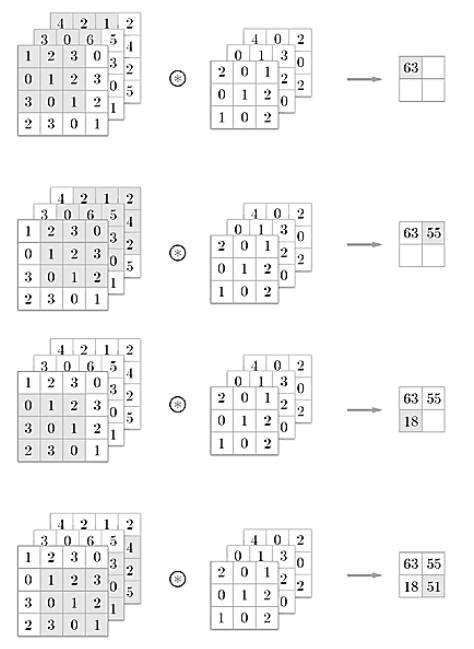
-3차원 데이터의 합성곱 연산 순서는 위 그림과 같음.

-주의 : 입력데이터 채널 수와 필터 채널 수가 같아야함 (위 그림에서는 3차원)

 

6. 블록으로 생각하기

 

합성곱 연산을 블록으로 표현한 것

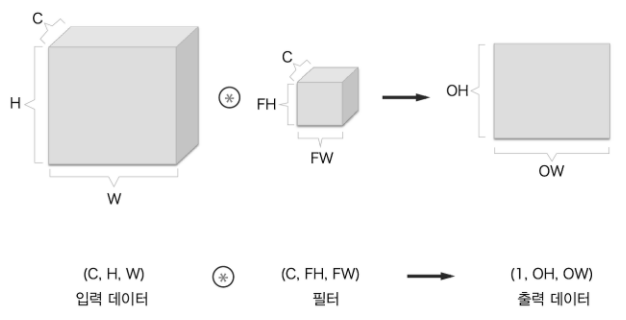
입력데이터 (C,H,W) * 필터(C, FH, FW) -> 출력데이터(1,OH,OW)

위와 같이 표현됨.

이때, 1차원(채널)으로 출력된다는 점을 알 수 있음

극복 방법? 필터를 여러 개 적용해주기.

 

 

필터를 여러 개 사용했을때의 합성곱 연산, 출력 데이터 형태.

입력데이터 (C,H,W) * 필터(FN, C, FH, FW) -> 출력데이터(FN,OH,OW)

드디어 위 그림과 같이 출력데이터가 1차원이 아니라 여러개 채널(FN)로 출력됨!

 

마지막 합성곱 연산에서 해줘야할 것이 뭐였지?

합성곱 연산에 편향을 추가함. 그 때 출력 데이터 형태

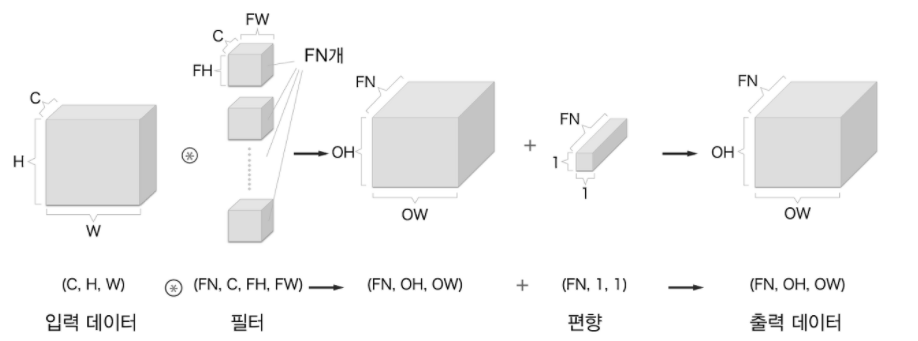
편향은 항상 1x1을 형태를 가지고 있다고 이전에 언급했음.

하지만 "채널은 같아야함"

그러므로 

출력데이터(FN, OH, OW) + 편향(FN, 1, 1) -> 최종 출력데이터(FN, OH, OW)

이와 같은 형태가 됨.

 

 

요약

-합성곱 연산은 완전 연결 계층의 1차원 출력 문제를 해결하기 위해 도입.

-합성곱 연산은 입력데이터에 필터를 연산하여 출력데이터를 만듦.
-출력 크기 조정을 위해 패딩을 사용하기도 함.

-합성곱 연산은 윈도우를 지정한 스트라이드만큼씩 옮기면서 연산함.

-3차원 데이터의 합성곱 연산 시 필터 또한 동일하게 3차원으로 사용.

-출력데이터를 다차원(또는 다채널)으로 만들고 싶으면 필터를 여러개 쓰면 됨.